Vectors
As discussed in the 1D kinematics lesson, vectors are quantities that consist of magnitude and direction whereas scalars are quantities involving magnitude only. Examples of vector quantities include displacement, velocity, acceleration, and force. Vector quantities are often represented by scaled vector diagrams.
Arrows are used to depict vectors and are drawn to scale in a specific direction. When drawing vector diagrams the scale is clearly listed and the arrow is drawn in a specific direction, thus, vectors have a head (arrowhead) and a tail.
The magnitude and direction are clearly labeled as shown below.
The direction of a vector is often expressed as an angle of rotation of the vector about its "tail" from either east, west, north, or south. The illustration below shows various directions as degrees counter-clockwise from East.
The magnitude of a vector is depicted by the length of the arrow which is drawn a precise length in accordance with a chosen scale (see example below).
Vector Addition
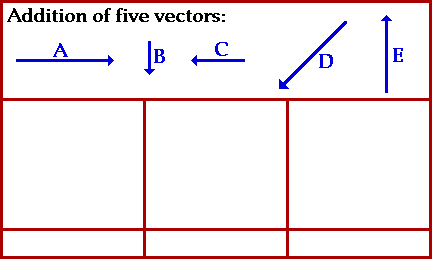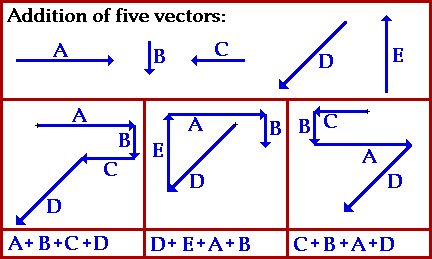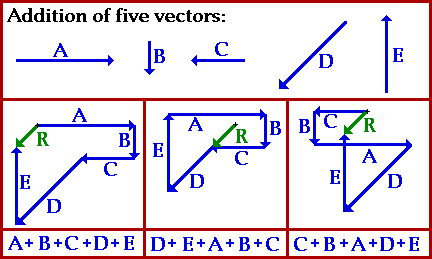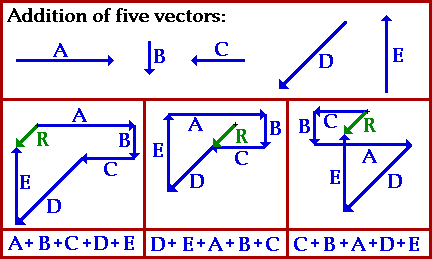
Two vectors can be added to together to determine the result (resultant). An example of adding vectors is shown below.
There are a variety of ways to determine the magnitude and direction of the resultant when vectors are directed in other than vertical or horizontal directions. The primary methods used are:
Pythagorean theorem and trigonometric methods
head-to-tail method using a scaled vector diagram
The Pythagorean is useful for determining the resultant of only two vectors which make a right angle to each other. This is illustrated below.
The example below illustrates the use of the Pythagorean theorem. Suppose you were to walk 11 km north from your house and then 11 km east. What would be your resulting displacement?
The direction of a particular vector can be determined through the use of trigonometric functions. The mnemonic SOH CAH TOA will help you remember the meaning of the three common trigonometric functions; sine, cosin, and tangent. The three equations below summarize these three functions in equation form.
Magnitude and direction of the sum of two or more vectors can also be determined by use of an accurately drawn head-to-tail diagram as illustrated below.
The resultant is drawn from the tail of the first vector to the head of the last vector (start to finish). Once drawn, the resultant length can be measured and converted to real units using the given scale. The direction of the resultant can be determined by using a protractor and measuring its counterclockwise angle of rotation from due East. Another example of the head-to-tail method is given below.
Using the head-to-tail method, the resultant (shown in red) is determined. Its magnitude and direction is labeled on the diagram.
Fundamentals
The resultant is the vector sum of two or more vectors. It is the result of adding vectors together. It may be said that vector R below is the resultant displacement of displacement vectors A, B, and C which means that if you walked with displacement A, then B, then C, you would be displaced the same amount as if you were displaced by R. Thus A + B + C = R (see below).
This concept is further illustrated by the diagram below.
Vector Components
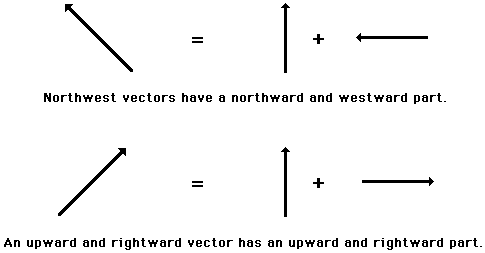
In situations where vectors are directed at angles to the customary coordinate axes, a useful math trick will be employed to transform the vector into two parts with each part being directed along the coordinate axis. For example, a vector which is directed northwest can be thought of as having two parts - a northward and a westward part.
Any vector directed in two dimensions can be thought of as having an influence in two different directions (parts). Each part of a two-dimensional vector is known as a component which depicts the influence of that vector in a given direction. The single two-dimensional vector could be replaced by the two components. This is illustrated below in the diagram involving walking a dog on a leash.
Now consider a picture hung on your wall. The wire, which forms a v-shape, exerts a tensional force both horizontally and vertically which are its components. We could say that the wire has a leftward and an upward tension.
Vector Resolution
The process of determining the magnitude of a vector is known as vector resolution. The two methods of vector resolution are:
parallelogram method
trigonometric method
The parallelogram method of vector resolution involves using an accurately drawn, scaled vector diagram to determine the components (sides of the parallelogram) using the scale. The parallelogram method of vector resolution performed as follows:
select a scale and accurately draw the vector to scale in the indicated direction.
sketch a parallelogram around the vector: beginning at the tail of the vector, sketch vertical and horizontal lines; then sketch horizontal and vertical lines at the head of the vector; the sketched lines will meet to form a parallelogram.
draw the components of the vector; the components are the sides of the parallelogram; be sure to place arrowheads on these components to indicate their direction (up, down, left, right).
label the components of the vectors with symbols to indicate which component is being represented by which side; a northward velocity component might be labeled vN ; etc.
measure the length of the sides of the parallelogram and use the scale to determine the magnitude of the components in real units; label the magnitude on the diagram.
The trigonometric method of vector resolution involves using trigonometric functions to determine components of the vector. It can be used to determine the length of the sides of a right triangle if one angle and the length of one side are known. This method is as follows:
construct a sketch of the vector in the indicated direction; label its magnitude and the angle which it makes with the horizontal.
draw a rectangle about the vector such that the vector is the diagonal of the rectangle; beginning at the tail of the vector, sketch vertical and horizontal lines; then sketch horizontal and vertical lines; then sketch horizontal and vertical lines at the head of the vector; the sketched lines will meet to form a parallelogram.
draw the components of the vector; the components are the sides of the rectangle; be sure to place arrowheads on these components to indicate their direction.
label the components of the vectors with symbols to indicate which component is being represented by which side; a northward force component would be labeled F-north and so forth.
use the sine function to determine the length of the side opposite the indicated angle; substitute the magnitude of the vector for the length of the hypotenuse; use some algebra to solve the equation for the length of the side opposite the indicated angle.
repeat the above step using the cosine function to determine the length of the side adjacent to the indicated angle.
The illustration below gives an example of this method.
Relative Velocity
Motion is relative to the observer. Occasionally, objects move within a medium which is moving with respect to an observer. For example, consider a plane flying with a crosswind. Using the usual methods of vector addition, it is possible to tell its actual direction and magnitude of motion as illustrated below.
Another example might involve a boat traveling across a river which has a crosscurrent. Using vector addition, it is also possible to determine the magnitude and direction of the boat as shown below.
Review Questions:
1. Hess takes flying lessons and is flying 80 mph. What is his speed if he encounters a 10 mph headwind?
70mph
2. What is Hess's speed if he encounters a 10 mph tailwind?
90 mph
3. What is Hess's speed if he encounter s a 10 mph crosswind?
80.6 mph
4. Ranada travels in a boat at 5 m/s East and encounters a current traveling 2.5 m/s, North. What is the resultant velocity of the motor boat?
5.59 m/s
5. If the width of the river is 80 meters wide, how much time does it take for Ranada to travel from shore to shore?
16.0 seconds
6. If Mathew is running with the football at 5 m/s East for a touchdown and a tackle from the opposing team pushes him 1.2 m/s, North. He is 80 meters from the endzone and 20 meters from the north sideline. Will he score a touchdown?
7. Suppose Jocelyn goes hang gliding and tries to land on the bulls eye of a target 120 meters straight ahead of her. She glides at 6 m/s, east (straight ahead) and encounters an air current of 3.8 m/s, south. How far off will she be, if any, from her target? At what angle would she need to adjust her next glide to hit the target in the center assuming all factors remain the same?
8. Trevor decides to go out for the swim team. To qualify, he must swim across the Colorado at a point that is 120 meters wide with an average speed of at least 7 m/s. The coach is unaware of currents and vectors. He swims at 6 m/s with a cross current of 3.8 m/s. Will Trevor qualify? Were there any factors that affected his qualifying or not qualifying?
20 seconds Yes. The cross current gave him a speed of 7.1 m/s which was faster than he was able to swim enabling him to qualify!
9. Suppose the current were 5 m/s in problem #8, how much time would be required for Trevor to swim across the same river? How far would he travel downstream during this time?
It would still take the same time but he would end up 100 m downstream!
10. Find the magnitude and direction for the resultant of the two forces: F1 = 100 N at an angle of 40 north of west and F2 = 200 N at an angle of30 west of south.
R = 208 N; angle 211.6 degrees